Hello there, today I thought to put out a blog for my future self—something which I want to look back to whenever I need to know anything about Big O. Also it will be getting updated as soon as I learn something new and that is really important to be added in here.

In this post, I'm just going to explain what these notations are about and why they're useful.

So now back to the topic.

Big O notation's concept

In computer science, Big O notation is used to describe how algorithms grow in runtime or space as the input size grows. In other words, it's a method for comparing the efficiency of various solutions to a problem.

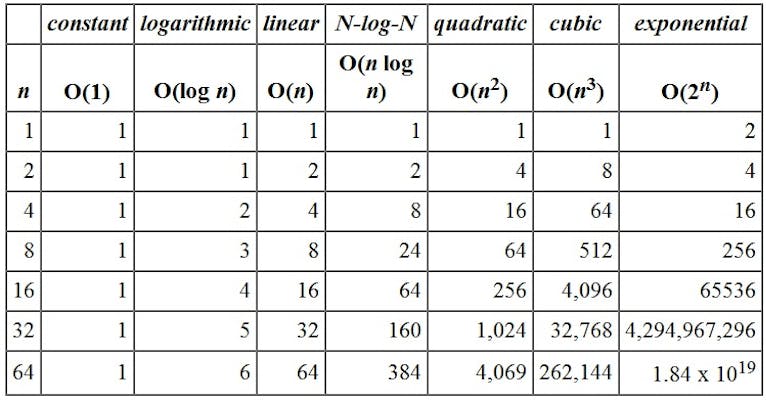
As you can see when the input size is really small the runtime is almost similar in all the cases but as soon as the input size grows we can notice the difference.

Few examples

The Constant Function f(n) = O(1)

void printSum(int a, int b)
{ 
  cout << a + b << endl;
}

Here this function runs in O(1) time (or "constant time") irrespective of its input size. It just takes a constant amount of time to do the sum.

Examples: arithmetic calculation, comparison, variable declaration, assignment statement

The Logarithm Function f(n) = O(log n)

int main()
{
    int i, n = 8;
    for (i = 1; i <= n; i=i*2) {
        cout << "Hello World " <<endl;
    }
    return 0;
}

Here we can see that the logarithm function gets slightly slower as n grows. Whenever n doubles, the running time increases by a constant.

Usually searching algorithms have log n if they are sorted i.e. Binary Search

The Linear Function f(n) = O (n)

void printSumofArray(int arr[], int size)
{ 
  int sum = 0;
  for(int i = 0 ; i < size ; i++){
    sum = sum + arr[i];  
  }
}

Here this function runs in O(n) time (or "linear time"), where size(n) is the number of elements in the array. It depends on the size(n) to calculate the sum of the array. Most of the Brute Force approaches.

The Quadratic Function f(n) = O (n^2)

void printPairs(int arr[], int n)
{ 
    // Nested loop for all possible pairs
    for (int i = 0; i < n; i++) {
        for (int j = 0; j < n; j++) {
            cout << "(" << arr[i] << ", "<< arr[j] << ")"<< ", ";
        }
    }
}

Quadratic algorithms are practical for relatively small problems. Whenever n doubles, the running time increases fourfold.

Example: some manipulations of the n by n array.

The Exponential Function f(n) = 2^n

int calFib(int n)
{
    if (n == 1 )
        return n;
    return calFib(n - 1) + calFib(n - 2);
}

It denotes an algorithm whose growth doubles with each addition to the input data set and this type of algorithm is usually not appropriate for practical use. Also about this block of code, I explained it in the Space complexity section.

Example: Tower of Hanoi... Also, it is known as the Tower of Brahma, and if you haven't read the story. I will definitely suggest reading. Just click here, I did the hard work for you

Space: The Final Frontier

The calculation of space complexity is very similar to the calculation of time complexity. Sometimes we prefer to minimize memory use over minimizing time. I still don't understand why though. Like how adding another variable will cause a drastic change in our code, which is the reason why I call it Insanity. Or maybe I still don't understand it, that is why I took the decision to write about it. I am really hoping that by the time I finish this essay on Space complexity you and I can fully understand it.

In case you are wondering what is Final Frontier and how it is related to Space complexity. For starters, it is Star Trek's reference, but also a bigger cause in between. Check this for more

When I started learning about it, I came across two terms space complexity and auxiliary space. Honestly, it took me a while to take hold of this concept, and for a good amount of time, I thought both of them were the same thing.

The auxiliary space is nothing but the space required by an algorithm during the execution of that algorithm. Space complexity does not equal auxiliary space, as input values are also included in space complexity.

Space Complexity = Auxiliary Space + Space used for input values

Fibonacci of a number (Recursive)

Let's look at the classic problem of computing the Fibonacci of numbers.

int calFib(int n)
{
    if (n == 1 )
        return n;
    return calFib(n - 1) + calFib(n - 2);
}

Image Credit

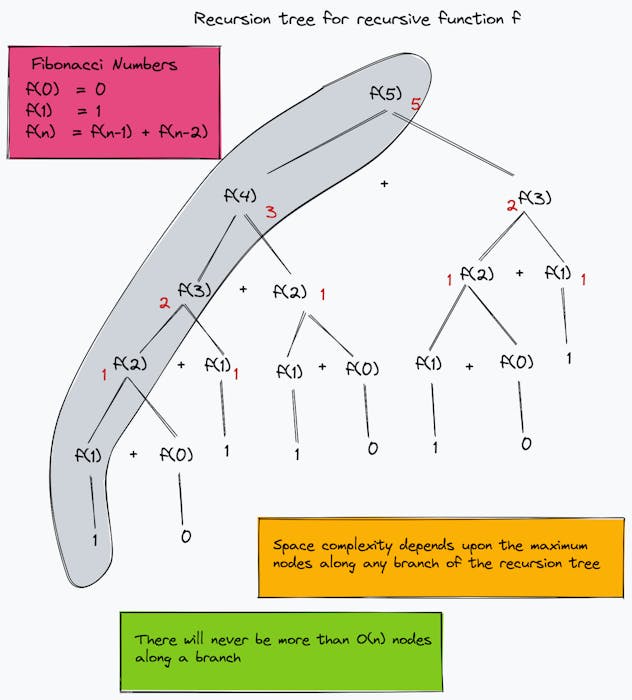
• Here, "n" is an integer variable that stores the value for which we have to find the Fibonacci, it will take "4 bytes" of space. i.e. n = 5

• Function calls, conditional statements, and return statements all come under the auxiliary space, and let's assume these all take up "4 bytes" of space.

• However, the reality is that it is calling the function recursively "n" times, so the complexity of auxiliary space is 4 * n bytes. Hence, the Total Space Complexity = (4 + 4*n) bytes but as we know that as we will drop the constants so that it gives us the complexity as O(n)

Mathematical Aspects or Proofs

Big O notation (with a capital letter O, not a zero), also called Bachmann–Landau notation or asymptotic notation. It comes from the names of the German mathematician Paul Bachmann and Edmund Landau who invented the notation. The letter O is used because the rate of growth of a function is also called its order.

Spoiler Alert: It's like math, except that it's an awesome, not-so-boring kind of math where you can trust your hands to handle the details and just let your mind wander to the task at hand.

Worst, Average, and Best Case Time

1. Best Case Time Complexity

2. Average Case Time Complexity:

3. Worst Case Time Complexity:

The art of explaining math is not my strong suit at the moment, but I will soon be able to do so.

How to Calculate the Big Oh

This is something that you will be able to figure out only when you do a good amount of DSA practice.

In the examples section, I did explain some of the examples of some of the important complexities and how to look for them. In a nutshell, these are the rules one must follow when finding TC and SC and we're usually talking about the "worst case"

• O(1): Constant time, mostly when there is not any kind of loop and you are just doing some calculations or comparisons or declaring another variable that is not needed or playing with hash tables or something more like link list insertion deletion.

• O(log N): Logarithmic. You know the array is sorted and you happen to see that some form of binary search is doing its magic, then you know it is log N or you are finding the smallest or largest in a binary search tree.

• O(n): Linear. All kinds of loops where you are accessing each element. Simply the loop goes on like 0 to n - 1. Linear Search is the best example here, but a bucket and counting sort operations can be also done in this.

• O(n log(n)): Linearithmic, usually introduced by bringing Divide and Conquer into consideration and sorting operations.

• O(n^2): Quadratic. Mostly when there is something with nested loops and every element in a collection needs to be compared to every other element. Not to forget the Bubble Sort, Insertion Sort, and Selection Sort.

• O(2^n): Exponential. Recursive algorithms that solve a problem of size N.

• O(n!): Factorial, happens when you are adding a loop for every single element.

Rules

1. Always about the "worst case"

2. Drop the constants

3. Different inputs should have different variables.

• A and B arrays nested would be O(a*b)

• A and B are for loops of the same function but different tasks O(a+b)

1. Drop the less significant terms

Practice Questions

int i, j, k = 0;
for (i = n / 2; i <= n; i++) {
    for (j = 2; j <= n; j = j * 2) {
        k = k + n / 2;
    }
}

Result: O(n Logn)

I love Big O analysis, except when I don't

While Bachmanity Insanity may have notable exceptions, it is unlikely you will use it every day. Mainly these are the problems that I faced with Big O

• Hardware differences — Runtime varies with the type of hardware on which the code is executing.

• Language differences — Even for the same algorithm, the execution time depends on what language the code is written in.

• Dropping Constants — It is told to drop the constants for example an algorithm takes 1000 (n log n) for a task vs another algorithm takes 20 (n log n) to do the same task but in the end, we can't say which is better as we drop the constants.

Maybe because it is not perfect, but it is the best way available to analyze an algorithm.

I have purposefully described these notations in an informal manner. If it does need correction feel free to correct me in the comments below.

This blog wouldn't have been possible without these, check these

• CS240

• GFG

• InterviewCake

• Don't forget to check this Legendary Big O cheat sheet

• Time and Space Complexity

• Also all the great programmers who made these memes, feel free to ask for the credit here.